Table of Contents:
Béla Bartók: Analysis of his music 1. (sheet music available)
Tonal Principles
The Axis System
“Every art has the right to strike its roots in the art of a previous. age; it not only has the right to but it must stem from it”, Bartok once declared.
His tonal system grew out of functional music. An uninterrupted line of evolution can be followed from the beginnings of functional . concepts, through the harmonies of Viennese classicism and the tone-world of romanticism to his axis system.
Best Sheet Music download from our Library.
By an analysis of his compositions, this axis system can primarily be shown to possess the essential properties of classical harmony, i.e.
(a) the functional affinities of the fourth and fifth degrees
ibr the relationship ofrelative major and minor keys
(cd _the overtone relations
( d) the role ofleading notes
.ei the opposite tension of the dominant and subdominant (/) the duality of tonal and distance principles
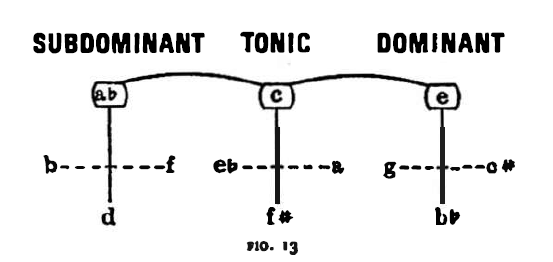
(a)To begin with, let us try to situate Bartók’s tonal system in the circle of fifths, Let us take C as the tonic (T). Then F, the fourth degree, is the subdominant (S); G, the fifth degree, ia the dominant (D); A, the sixth degree and relative of the tonic, functions as a tonic; D, the second degree, and relative of the subdominant, functions as a subdominant; E, the third degree and relative of the dominant, functions as a dominant. The series of fifths, F-C-G-D-A-E corresponds to the functional series S-T-D-S-T-D.
Please, subscribe to our Library. Thank you!
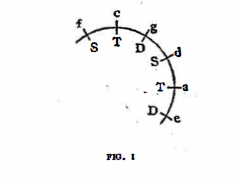
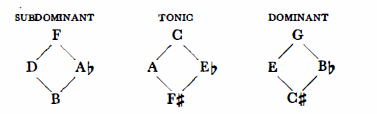
We note that the sequence S-T-D repeats itself. When this periodicity is extended over the entire circle of fifths the scheme of the axis system may be clearly seen:
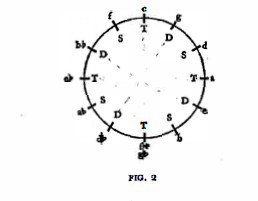
Let us separate the three funtions and call them tonic, subdominant dominant and dominant axes, respectively.
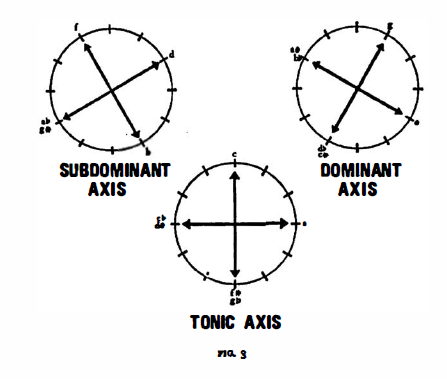

This table teaches yet another lesson. All four movements rest on the tonic axis, A-C-Eb-F#. Thus the first and fourth movements are supported by the “principal branch”, A and Eb,; the middle movements, however, by the “secondary branch”, C and F#, Thus each axis has a two-fold affinity depending on whether we oppose the pole with the counterpole, or the principal branch with the secondary branch.
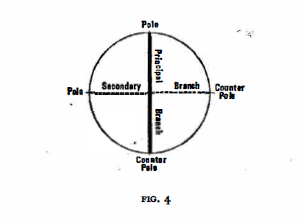
Consequently the components of the axis system are as follows:

The Slow Movement of the Sonata for Two Pianos and Percussion is based on the subdominant axis, B-D-F-Ab, complying with the traditions of classical composition. The modal arrangement of its principal theme is symmetrical: the beginning and end supported by the B and F counterpoles (i.e. the principal branch of the axis).

b) A survey of the evolution of harmonic thinking leads to the
conclusion that the birth of the axis system was a historical
necessity, representing the logical continuation (and in a _<:ertain sense the completion) of European functional music. It can be demonstrated that the axis system, with its characteristic features had, in effect, been used by the Viennese “Greats”. Indeed, it had been recognised by Bach, in his chromaticism.
The sense of functional correlation in music was introduced in practice by the realisation of the I-IV-V-I affinity (in medieval modal music, at first in cadence form only) In the case of the C tonic:
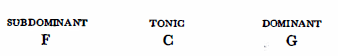
The classical theory of harmony already speaks of primary and secondary triads inasmuch as the C may be replaced by its relative A, the F by its relative D and the G by its relative E.
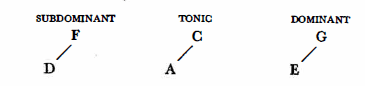
Romantic harmony goes still further, making frequent use of the upper relatives. (Naturally only major and minor keys of similar key signature may be regarded as relatives, e.g. C major and A minor, or C minor and Eb major):
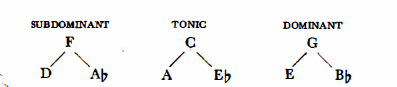
One more step completes the system. The axes extend the application of relatives to the whole system. The axis system implies the recognition of the fact that the common relative for A and Eb, is not only C, but also F# ( =Gb); that D and Ab, not only have F as a common relative, but also B; and that E and Bb, not only have G, but also C# ( =Db) as common relatives.
As is well known, Bartók showed a preference for the use ofso-called majoMninor chords (see Fig. 32b). For instance, its form in C tonality is:

The function remains unchanged even if the C major modeas shown in the above chord-is replaced by the relative A minor, or when the Eb major tonality replaces the relative C minor. This technique occurs regularly in Bartók’s music:
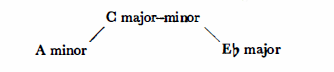
These substitute chords may also be employed in major-minor form, which brings the system to a close, since the relative of A major (F# minor) and that, of Eb, minor (Gb major) meet at a point of enharmonic co.incidence, F#=Gb.
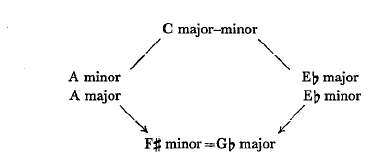
These relatives, applied to dominant and subdominant harmony, again result in the scheme of the axis system.
(c) The theory of the axis system is also substantiated by the laws of acoustics. Acoustically, arriving from the dominant to the tonic, is to reach the root from an overtone-all cadential relations rest on the principle of interconnection between roots and their overtones. Thus, the dominant of C is not only G but also the next overtones E and Bb. Therefore the circle of tonic-dominant relationships is expanded to include E-C and Bb-C.
Since the D-T relationship corresponds relatively to
the T-S and
the S-D relationship,
overtone-root attraction exists between the T-S and the S-D, as well.
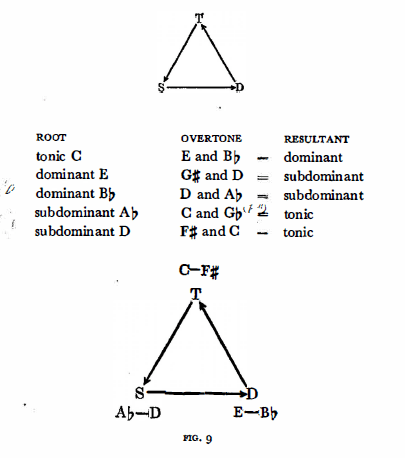
If we add the role of the nearest overtone, i.e. the fifth, then we
can deduce the complete axis system from these relations.
(d) In the simplest cadence, that of V7-I, the main role is played by the so-called sensitive notes which produce the pull of the dominant towards the tonic. The leading note pulls to the root and the seventh towards the third degree of the tonic, i.e. the leading note B resolves on C ind the seventh F on E or Eb.

These important sensitive notes bear a tritonic relationship to each other. The tritone–half the octave interval-is characterised by the interchangeability of its notes without changing the interval. Thus, if the B-F relationship is converted into an F-B one (as is frequently the case with Bartók), then the F ( =E#) assumes the role of the leading note, pulling towards the F# instead of E, while the seventh B pulls towards A# or A instead of C. So, instead of the expected tonic C major, the counterpole, the equally tonic F# major (or minor) emerges.

This resolution is reserved by Bartók for a sudden change of scene. The circumstances of an expected G7-C cadence emerging as G7-F# gives us a “Bartokean pseudo-cadence”.
(e) Starting from the tonic centre C we reach the dominant in one direction and the subdominant in the other, in identical latitudes. At a distance of i fifth we find the dominant G upwards and the subdominant F downwards. Regarding overtone relations we also get the dominant G, E, Bb, in the upper and the subdominant F, Ab, D the lower directions.
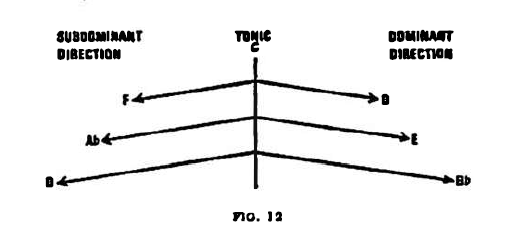
But what happens if the pendulum covers the latitude of a tritone? In this case the deviations made upwards and downwards meet, both ending at F# ( =Gb), and ifwe were to take one as the dominant, then the other would have to assume the subdominant function. By this coincidence, however, a neutralisation of their functions takes place, dominant and subdominan t merging are rendered ineffective in the interaction of their opposite forces.
Consequently the balance is saved, and the function is invariably that of the tonic. The counterpole is born. Similarly the distance between the tonic C and F# is bisected by Eb ( =D#) in the one and by A in the other direction; so lying in tensionless, neutral section points, they also have to be interpreted as tonics,. No more than four tonic poles can be surmised, since the intervals C-Eb, Eb-F#, F#-A, A-C provide no further points of bisection.
Finally, what significance should be attached to a swing of a chromatic degree, of C-B and its counterpart C-C# (=Db,)? Which is then to assume the dominant and which the subdominant function? Related to B, C# shows a degree of elevation of two fifths, which might correspond to the S-D interdependence, but not to its opposite. Anyway, the subdominant function of B and the dominant function of C# are unquestionable when they are related to the tonic F# counterpole.
(f) Thus, observing the logic of functional interconnection of the three axes, another interesting point arises. The subdominant and dominant are represented most effectively not by the degrees IV and V but, in the case of C tonality, the subdominant by Ab, (and its counterpole), the dominant by E (and its counterpole).
This is, after all, nothing new since there is, for instance, the dominant secondary theme in E of Beethoven’s Waldstein Sonata (C major) or the subdominant Slow Movement in Ab, of the Pathetique (C minor). The movements of Brahms’ First Symphony have the following key-sequence: C-E-Ab,-C in the sense of tonic-dominant-subdominant-tonic, etc.
However, the above examination of the axis system fails to explain why Bartók prefers these augmented triad relations to the traditional I-IV-V-I.
This necessitates a new approach to the system.
It is generally accepted that twelve-tone music shows a strong tendency to indifferent tonal relations.
Atonal relations can be most suitably effected by the equal division of the octave, or of the circle of fifths. By dividing the octave m twelve equal parts we get the chromatic scale; in the case of six equal parts we have the whole-tone scale; four equal parts gives us the chord of the diminished seventh; three the augmented triad, and finally by dividing the octave into two equal parts we arrive at the tritone.
For the present we shall exclude the whole-tone scale because of its limited possibilities: two whole-tone scales produce the chromatic scale by interlocking.
Every tonal system presupposes a centre as well as subordinate relations dependent on the centre. Taking again C as the tonic centre, the three functions are represented most potently by those degrees dividing the circle of fifths into three equal parts, i.e. in the augmented triad C-E-Ab. Properties inherent in classical harmony are responsible for the E assuming a dominant function and Ab, a subdominant function in relation to the tonic C.
Each of these main notes permit their substitution by their counterpoles, i.e. their tritonic equivalents. Thus, C may be replaced by F#, E by Bb, and Ab by D.
If we divide the twelve-tone chromatic scale proportionally between the three functions, each function will have four poles, and these-insofar as we keep to the distance principle-are arranged in diminished-seventh relations, dividing the circle into four equal parts. Accordingly, C-Eb-F#-A belong to the range of the C tonic, E-G-Bb-C# to that of the dominant E main note, and Ab-B-D-F to that of the subdominant Ab, main note.
So, the tonal system resulting from a division of the chromatic scale into equal parts agrees completely with the axis system:
Put concisely, given the twelve-tone system and the three functions this is the on[y system that can be realised by means of distance division.
Viewed historically, the axis system reflects the age-old struggle between the principles-of tonaliry and equi-distance, with the gradual ascendancy of the latter which finally resulted in the free and equal treatment of the chromatic twelve notes.
Here we have to draw a line between Bartók’s twelve-tone system and the Zwölftonmusik of Schönberg. Schönberg annihilates and dissolves tonality whereas Bartók incorporates the principles of harmonic thinking in a perfect synthesis. To penetrate into Bartók’s creative genius is to discover the natural affinities and intrinsic possibilities, inherent in the musical material.
